The physics of small earthquakes
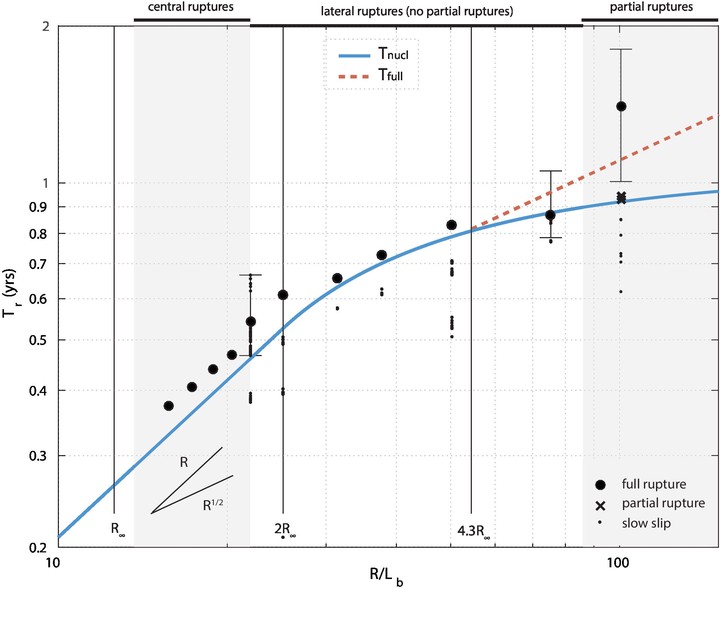 Comparison between numerical simulations (dots) and analytical results (blue line), showing the scaling observed in nature. From Cattania and Segall, 2018 (link)
Comparison between numerical simulations (dots) and analytical results (blue line), showing the scaling observed in nature. From Cattania and Segall, 2018 (link)
Small repeating earthquakes are events characterized by very similar waveforms, and overlapping rupture areas. Unlike most other earthquakes, they are very periodic; they are commonly interpreted as rupturing an isolated asperity embedded in a velocity-strengthening (creeping) fault. Since they are driven by aseismic slip, they are an invaluable tool to probe creeping sections of a fault, and detect spatio-temporal variations in slip rate. I used simple crack models to derive analytical expressions for the recurrence interval as a function of asperity dimension and seismic moment. These expressions are in excellent agreement with the scaling between recurrence interval and seismic moment observed in the simulations: $T_r \sim M_0^{1/ 6}$ (see figure), consistent with observations.
While these results are based on a relatively simple model (circular, uniform asperities), they provide a useful framework to interpret the seismic behavior of small asperities. They make specific predictions, such as a dependence of stress drop on magnitude and a transition between central ruptures for small asperities to lateral ruptures for large asperities (where small and large is a well defined ratio between the asperitity radius and the nucleation radius); similarly, the occurrence of partial ruptures is expected for asperities exceeding a particular dimension.
Cattania, C. and P. Segall (2018), Crack models of repeating earthquakes predict observed moment-recurrence scaling, J. Geophys. Res. Solid Earth ( abstract; article)
Current and future efforts: The results above imply a break of self-similarity near the nucleation dimension. Could this be seen in the data? To answer this question, we first need a theoretical source model for small earthquakes, which does not assume constant rupture velocity but instead considers the initial acceleration. I will present some preliminary results on this topic at the 2020 AGU Fall Meeting.